Frameworks like React and Vue.js made a big impact in Web front-end by incorporating reactive programming, which allows writing dynamic UI code in an automatic, declarative way. However, the lineage of ideas that inspired them can get pretty muddled. In Evan You’s 2016 dotJS talk, he “instantly regretted” using the word reactivity in his title because of the “endless confusion of what reactive actually means.”

Definition policing is boring, but in this case there’s some actual interesting stuff that gets lost in the confusion. When you trace back to older ideas like functional reactive programming (FRP) from 1996, you see that most reactive systems in use today—even those that explicitly call themselves FRP—lack important abstractions which prevent writing buggy, inconsistent code.

Reactivity at its simplest looks something like a spreadsheet. A cell is a reactive value. Cells are either plain containers which you manually change, or they are formulae like SUM(A1:A9) which combine other cells together in an expression. Formulae automatically recompute when dependent cells change.

A system like this is easy to implement and has great properties. First, formulae have no side-effects, so when a cell changes, the order that dependent formulae are updated doesn’t matter because they don’t affect anything. Because of this, it’s also “glitch-free”: the whole sheet is essentially updated in one transaction; no intermediate, partial states have any effect.

However, outside frameworks, the reactivity primitive programmers are more likely to have encountered is the observable, popularised by the ReactiveX libraries. Observables are streams which can be connected together and subscribed to. Crucially, they aren’t like spreadsheets; they are far looser. In spreadsheets, each cell has a current value. Observables don’t have current values; they’re streams.

We can represent spreadsheets with observables, though, which most libraries do. We need to interpret a stream as a stream of updates to the value, or of samples of a value over time. Plain cells are just plain observables which we send values through. And to make formulae, we can use the CombineLatest ReactiveX operator, which continually collects the latest values from all its input observables, runs them through a function, and emits the result.

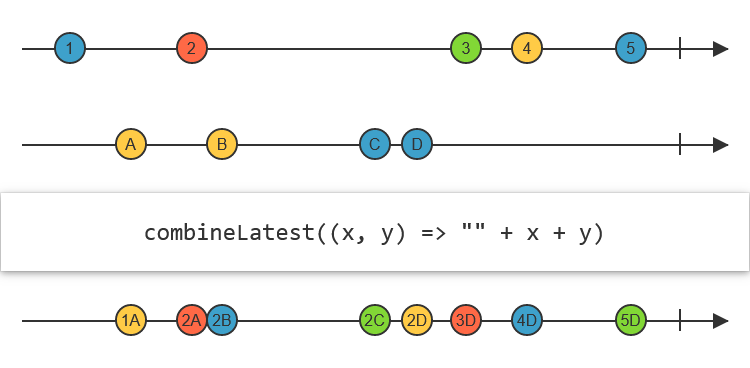
Problem solved, right?

Wrong! By building the system around a stream of updates, we’ve thrown out the guarantees we got from a spreadsheet.

First, updates can cause side-effects. Observables can be subscribed to with arbitrary functions, which could interfere with each other: this means that the order they run in is important and can lead to different results. Picture two subscriptions which send values through the same observable: their running order now affects the order of events going through the system.

Second, because of this, the system is no longer glitch-free. Suppose we have a formula with two inputs, like X + Y. If both X and Y change in response to the same thing, their updates still happen one at a time, so it causes two separate updates to be emitted from the formula observable. The first of these formula updates is an intermediate state which shouldn’t be seen; only one of X or Y has its new value, even though both were supposed to change at the same time. Subscriptions downstream of the formula, like UI updates, will process invalid state.

Lastly, the system is sample-rate dependent. In classic FRP, values are considered to continuously vary; the fact they “update” in steps is just an unfortunate detail of implementation. So, being sample-rate independent means that the updates actually model a continuous process: if we sample more or less frequently, it doesn’t change the meaning of anything in the system. Sampling more frequently should converge us closer and closer to the true, continuously-varying value. For example, if a cell observable re-emits the same value with no changes, nothing should happen anywhere else. A formula which counts the number of input samples is not sample-rate independent. Neither is a formula which reduces/folds samples. However, observable-based libraries let you write these with no restriction. BaconJS, for example, has a type representing a reactive value, but lets you reduce it and subscribe to it.

To fully avoid these problems, a library needs to do two things:

• Defer subscriptions: allow multiple cells to update and finish propagating changes before running subscriptions. For example, MobX’s Reactions run after all input actions (transactions) have finished.

  Notably, this means you cannot implement formulae with your API’s subscription mechanism. You need a different, internal system to propagate changes.

• Enforce/encourage sample-rate independence: custom cell formula functions should be stateless and free of side-effects, including changing other cells.

  If you want something like “cells with state” in your system, do it the FRP way and add a separate type for discrete event streams. This should be unrelated to your type for normal cells; cells are not just events which save their last values. E.g. events can be counted, but cell changes can’t. Events cannot respond to cell changes, but stateful event pipelines can be built, just like observables, which then feed into cells.

  You may wish to have actual cells with state, as long as they are continuous / sample-rate independent; e.g. integrals.

Making the updating process explicit and transactional in this way makes the reactive system far more expressive. For an example, check out Yampa for Haskell. (👀 Yampa has some other powerful operators unseen in Web libraries which I will cover in a later post, so make sure to subscribe!)

Unfortunately though, ideas like reactive events and safe stateful cells don’t seem to have made it big in the Web space, or even non-functional languages. MobX, for example, doesn’t handle events, leaving that work to your external, non-reactive code.

Could it be a useful improvement? I’m experimenting with the idea in Python at refs.py and refs_gl.py.